Serie – Gruppo Esercizi 3

Esercizi Proposti da prof. Franco Franceschini - Lug 5, 2012 Serie 0 0 Views : 7108 Receive Updates For This Category

Like This Article

Article Tools

Print this page
Add Comment
Send to Friend
Share This
Last Updated on :
Lug 9, 2012

Esercizio 1

Calcolare $\displaystyle x \in \mathbb{R}$ tale che

$\displaystyle \sum_{n=2}^{+ \infty }\; \; 2\left ( x+1 \right )^{n}+\sum_{n=1}^{+ \infty }\; \;\left ( x \right )^{n}=\frac{2x^{2}}{1-x}$

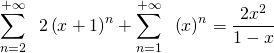
Qui trovi la soluzione.

Visiona e acquista le nostre dispense di Matematica complete di Teoria ed Esercizi scritte da un professore di grande esperienza.

Scopri il nostro Video Corso "Didattica Inclusiva DSA e BES" utilissimo per genitori, insegnanti, psicologi, logopedisti, educatori ed altri professionisti che desiderano una formazione di base sui principali aspetti clinici relativi ai BES ed ai DSA e sulle esigenze concrete degli alunni.

Tutte le informazioni sul Video Corso sul sito: www.videocorsodsaebes.it

i contenuti di questo sito sono curati dagli specialisti del
Centro Sapere Più - a Milano dal 1996 al servizio di chi studia